சைன் விதி எனப்படுவது திரிகோண கணிதத்திலும் ஏனைய முக்கிய கணிப்புக்களிலும் பயன்படுத்தப்படும் ஒரு விதியாகும். இது முக்கோணமொன்றின் பக்கங்களுக்கும், அதன் கோணங்களின் சைன் பெறுமதிகளுக்கும் இடையிலான தொடர்பைக் காட்டுகிறது.
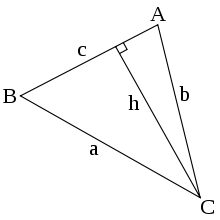
சைன் விதியை விளக்கும் முக்கோணி யாதுமொரு முக்கோணி ABCயில்,
a
sin
A
=
b
sin
B
=
c
sin
C
{\displaystyle {\frac {a}{\sin A}}\,=\,{\frac {b}{\sin B}}\,=\,{\frac {c}{\sin C}}}
கூர்ங்கோண முக்கோணியில் சைன் விதி இம்முக்கோணியில் செங்குத்துயரம் hஐச் சமப்படுத்தினால்,
a
s
i
n
B
=
b
s
i
n
A
{\displaystyle asinB=bsinA}
ஆகவே,
a
sin
A
=
b
sin
B
{\displaystyle {\frac {a}{\sin A}}\,=\,{\frac {b}{\sin B}}\,}
A உச்சியிலிருந்து செங்கோடு வரைந்து அதன் மதிப்புகளை இதே வகையில் கண்டறிந்து சமப்படுத்தினால்
c
s
i
n
B
=
b
s
i
n
C
{\displaystyle csinB=bsinC}
ஆகவே,
b
sin
B
=
c
sin
C
{\displaystyle {\frac {b}{\sin B}}\,=\,{\frac {c}{\sin C}}\,}
இவை இரண்டையும் இணைத்தால்
a
sin
A
=
b
sin
B
=
c
sin
C
{\displaystyle {\frac {a}{\sin A}}\,=\,{\frac {b}{\sin B}}\,=\,{\frac {c}{\sin C}}}
விரிகோண முக்கோணியில் சைன் விதி இம்முக்கோணியில் செங்குத்துயரத்தைச் சமப்படுத்தினால்,
a
s
i
n
(
180
−
B
)
=
b
s
i
n
A
{\displaystyle asin(180-B)=bsinA}
a
s
i
n
B
=
b
s
i
n
A
{\displaystyle asinB=bsinA}
ஆகவே,
a
sin
A
=
b
sin
B
{\displaystyle {\frac {a}{\sin A}}\,=\,{\frac {b}{\sin B}}\,}
A உச்சியிலிருந்து செங்கோடு வரைந்து அதன் மதிப்புகளை இதே வகையில் கண்டறிந்து சமப்படுத்தினால்
c
s
i
n
B
=
b
s
i
n
C
{\displaystyle csinB=bsinC}
ஆகவே,
b
sin
B
=
c
sin
C
{\displaystyle {\frac {b}{\sin B}}\,=\,{\frac {c}{\sin C}}\,}
இவை இரண்டையும் இணைத்தால்
a
sin
A
=
b
sin
B
=
c
sin
C
{\displaystyle {\frac {a}{\sin A}}\,=\,{\frac {b}{\sin B}}\,=\,{\frac {c}{\sin C}}}
[ தொகு ] சைன் விதியின் விகிதங்களின் பொதுமதிப்பு சுற்றுவட்டத்தின் விட்டத்திற்குச் சமமென வருவித்தலுக்கான படம்.
a
sin
α
=
b
sin
β
=
c
sin
γ
,
{\displaystyle {\frac {a}{\sin {\alpha }}}={\frac {b}{\sin {\beta }}}={\frac {c}{\sin {\gamma }}},}
சுற்றுவட்டத்தின் விட்டத்திற்குச் சமமாக இருக்கும். இந்த முடிவு கணிதவியலாளர் தொலெமி காலத்திலேயே அறியப்பட்டிருந்தது.[ 1] [ 2]
△
A
B
C
{\displaystyle \triangle ABC}
O வழிச் செல்லும் முக்கோணம்
△
A
D
B
{\displaystyle \triangle ADB}
∠
A
B
D
=
90
∘
{\displaystyle \angle ABD=90^{\circ }}
இப்போது
△
A
B
D
{\displaystyle \triangle ABD}
sin
δ
=
opposite
hypotenuse
=
c
2
R
,
{\displaystyle \sin {\delta }={\frac {\text{opposite}}{\text{hypotenuse}}}={\frac {c}{2R}},}
R
=
d
2
{\displaystyle R={\frac {d}{2}}}
[ 2]
γ
=
δ
{\displaystyle {\gamma }={\delta }}
sin
δ
=
sin
γ
=
c
2
R
.
{\displaystyle \sin {\delta }=\sin {\gamma }={\frac {c}{2R}}.}
இதனை மாற்றியமைக்க:
2
R
=
c
sin
γ
.
{\displaystyle 2R={\frac {c}{\sin {\gamma }}}.}
△
A
D
B
{\displaystyle \triangle ADB}
2
R
{\displaystyle 2R}
a
sin
α
=
b
sin
β
=
c
sin
γ
=
2
R
.
{\displaystyle {\frac {a}{\sin {\alpha }}}={\frac {b}{\sin {\beta }}}={\frac {c}{\sin {\gamma }}}=2R.}
[ தொகு ] முக்கோணத்தின் பரப்பளவு வாய்பாடு
T
=
1
2
a
b
sin
θ
{\textstyle T={\frac {1}{2}}ab\sin \theta }
a b
θ
{\displaystyle \theta }
sin
θ
{\displaystyle \sin \theta }
R
{\displaystyle R}
[ 3]
T
=
1
2
a
b
⋅
c
2
R
.
{\displaystyle T={\frac {1}{2}}ab\cdot {\frac {c}{2R}}.}
T
=
a
b
c
4
R
.
{\displaystyle T={\frac {abc}{4R}}.}
இதிலிருந்து மேலும் பெறக்கூடிய வாய்பாடுகள்:
a
b
c
2
T
=
a
b
c
2
s
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
=
2
a
b
c
(
a
2
+
b
2
+
c
2
)
2
−
2
(
a
4
+
b
4
+
c
4
)
,
{\displaystyle {\begin{aligned}{\frac {abc}{2T}}&={\frac {abc}{2{\sqrt {s(s-a)(s-b)(s-c)}}}}\\[6pt]&={\frac {2abc}{\sqrt {{(a^{2}+b^{2}+c^{2})}^{2}-2(a^{4}+b^{4}+c^{4})}}},\end{aligned}}}
T s
s
=
a
+
b
+
c
2
.
{\textstyle s={\frac {a+b+c}{2}}.}
அரைச்சுற்றளவு இரண்டாவது வாய்பாட்டை முக்கோணப் பரப்பளவுக்கான ஈரோனின் வாய்பாடாக சுருக்கலாம்.
சைன் விதியைக் கொண்டு கீழ்வரும் முக்கோணப் பரப்பளவிற்கான வாய்பாட்டைப் பெறலாம்:
S
=
sin
A
+
sin
B
+
sin
C
2
{\textstyle S={\frac {\sin A+\sin B+\sin C}{2}}}
[ 4]
T
=
4
R
2
S
(
S
−
sin
A
)
(
S
−
sin
B
)
(
S
−
sin
C
)
{\displaystyle T=4R^{2}{\sqrt {S\left(S-\sin A\right)\left(S-\sin B\right)\left(S-\sin C\right)}}}
. (
R
{\displaystyle R}
2
R
=
a
sin
A
=
b
sin
B
=
c
sin
C
{\textstyle 2R={\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}}
ஒரு கோளத்தின் பெருவட்டங்களின் விற்களைப் பக்கங்களாகக் கொண்டு அக்கோளத்தின் மீதமையும் முக்கோணங்கள் கோள முக்கோணங்களாகும்.
ஓரலகு ஆரமுள்ள கோளத்தின் மீதமைந்த முக்கோணத்தின் பக்க நீளங்கள் a b c A B C
sin
A
sin
a
=
sin
B
sin
b
=
sin
C
sin
c
.
{\displaystyle {\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}.}
கோள முக்கோணத்தின் பக்கங்கள் கோளத்தின் ஆரத்தைவிட மிகச் சிறியதாக இருக்கும்போது இவ்விதியானது கிட்டத்தட்ட தள முக்கோணவியலின் சைன் விதியை ஒத்திருக்கும்.
சைன் விதியின் நிறுவல் கீழுள்ளவாறு டோதுந்தேரின் நூலில் உள்ளது.[ 5]
sin
2
A
=
1
−
cos
2
A
{\displaystyle \sin ^{2}A=1-\cos ^{2}A}
cos
A
{\displaystyle \cos A}
sin
2
A
=
1
−
(
cos
a
−
cos
b
cos
c
sin
b
sin
c
)
2
=
(
1
−
cos
2
b
)
(
1
−
cos
2
c
)
−
(
cos
a
−
cos
b
cos
c
)
2
sin
2
b
sin
2
c
sin
A
sin
a
=
[
1
−
cos
2
a
−
cos
2
b
−
cos
2
c
+
2
cos
a
cos
b
cos
c
]
1
/
2
sin
a
sin
b
sin
c
.
{\displaystyle {\begin{aligned}\sin ^{2}A&=1-\left({\frac {\cos a-\cos b\cos c}{\sin b\sin c}}\right)^{2}\\[5pt]&={\frac {(1-\cos ^{2}b)(1-\cos ^{2}c)-(\cos a-\cos b\cos c)^{2}}{\sin ^{2}\!b\,\sin ^{2}\!c}}\\[5pt]{\frac {\sin A}{\sin a}}&={\frac {[1-\cos ^{2}\!a-\cos ^{2}\!b-\cos ^{2}\!c+2\cos a\cos b\cos c]^{1/2}}{\sin a\sin b\sin c}}.\end{aligned}}}
இம்முடிவின் வலப்பக்க மதிப்பில்
a
,
b
,
c
{\displaystyle a,\;b,\;c}
sin
B
sin
b
=
[
1
−
cos
2
a
−
cos
2
b
−
cos
2
c
+
2
cos
a
cos
b
cos
c
]
1
/
2
sin
a
sin
b
sin
c
{\displaystyle {\frac {\sin B}{\sin b}}={\frac {[1-\cos ^{2}\!a-\cos ^{2}\!b-\cos ^{2}\!c+2\cos a\cos b\cos c]^{1/2}}{\sin a\sin b\sin c}}}
sin
C
sin
c
=
[
1
−
cos
2
a
−
cos
2
b
−
cos
2
c
+
2
cos
a
cos
b
cos
c
]
1
/
2
sin
a
sin
b
sin
c
{\displaystyle {\frac {\sin C}{\sin c}}={\frac {[1-\cos ^{2}\!a-\cos ^{2}\!b-\cos ^{2}\!c+2\cos a\cos b\cos c]^{1/2}}{\sin a\sin b\sin c}}}
ஃ
sin
A
sin
a
=
sin
B
sin
b
=
sin
C
sin
c
.
{\displaystyle {\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}.}
அலகு கோளத்தின் மையம் O OA OB OC a . OA ஐ z -அச்சிலும், xz -தளத்தில் OB ஆனது z -அச்சுடன் உருவாக்கும் கோணம் c எனவும் கொண்டு ஒரு கார்ட்டீசியன் அடுக்களத்தை எடுத்துக்கொள்ள, xy - தளத்தில் OC இன் வீழல் ON ஆகவும், ON, x -அச்சுக்கு இடைப்பட்ட கோணம் A ஆகவும் இருக்கும். எனவே OA , OB , OC திசையன்களின் கூறுகள் பின்னுள்ளவாறு அமையும்:
O
A
=
(
0
0
1
)
,
O
B
=
(
sin
c
0
cos
c
)
,
O
C
=
(
sin
b
cos
A
sin
b
sin
A
cos
b
)
.
{\displaystyle \mathbf {OA} ={\begin{pmatrix}0\\0\\1\end{pmatrix}},\quad \mathbf {OB} ={\begin{pmatrix}\sin c\\0\\\cos c\end{pmatrix}},\quad \mathbf {OC} ={\begin{pmatrix}\sin b\cos A\\\sin b\sin A\\\cos b\end{pmatrix}}.}
(
O
A
⋅
(
O
B
×
O
C
)
)
2
=
(
det
(
O
A
O
B
O
C
)
)
2
=
|
0
0
1
sin
c
0
cos
c
sin
b
cos
A
sin
b
sin
A
cos
b
|
2
=
(
sin
b
sin
c
sin
A
)
2
.
{\displaystyle {\begin{aligned}{\bigl (}\mathbf {OA} \cdot (\mathbf {OB} \times \mathbf {OC} ){\bigr )}^{2}&=\left(\det {\begin{pmatrix}\mathbf {OA} &\mathbf {OB} &\mathbf {OC} \end{pmatrix}}\right)^{2}\\[4pt]&={\begin{vmatrix}0&0&1\\\sin c&0&\cos c\\\sin b\cos A&\sin b\sin A&\cos b\end{vmatrix}}^{2}=\left(\sin b\sin c\sin A\right)^{2}.\end{aligned}}}
OA ⋅ (OB × OC )திசையிலி முப்பெருக்கத்தின் மதிப்பு, OA , OB , OC இணைகரத்திண்மத்தின் கனவளவுக்குச் (V OA OB OC
z OB (sin c sin a sin B )2 எனவும், z OC (sin a sin b sin C )2 எனவும் கிடைக்கும். மூன்று விடைகளையும் சமப்படுத்தி, (sin a sin b sin c )2 ஆல் வகுக்க:
sin
2
A
sin
2
a
=
sin
2
B
sin
2
b
=
sin
2
C
sin
2
c
=
V
2
sin
2
(
a
)
sin
2
(
b
)
sin
2
(
c
)
,
{\displaystyle {\frac {\sin ^{2}A}{\sin ^{2}a}}={\frac {\sin ^{2}B}{\sin ^{2}b}}={\frac {\sin ^{2}C}{\sin ^{2}c}}={\frac {V^{2}}{\sin ^{2}(a)\sin ^{2}(b)\sin ^{2}(c)}},}
கோளத்தின் ஆரம் ஓரலகு எனில்,
O
A
=
O
B
=
O
C
=
1
{\displaystyle OA=OB=OC=1}
∠
A
D
O
=
∠
A
E
O
=
90
∘
{\displaystyle \angle ADO=\angle AEO=90^{\circ }}
D
,
{\displaystyle D,}
E
{\displaystyle E}
∠
A
′
D
O
=
∠
A
′
E
O
=
90
∘
{\displaystyle \angle A'DO=\angle A'EO=90^{\circ }}
A
′
{\displaystyle A'}
இதிலிருந்து
∠
A
D
A
′
=
B
,
{\displaystyle \angle ADA'=B,}
∠
A
E
A
′
=
C
{\displaystyle \angle AEA'=C}
A
′
{\displaystyle A'}
O
B
C
{\displaystyle OBC}
A
{\displaystyle A}
∠
A
A
′
D
=
∠
A
A
′
E
=
90
∘
{\displaystyle \angle AA'D=\angle AA'E=90^{\circ }}
முக்கோணவியலின் அடிப்படைப் பண்புகளின்படி:
A
D
=
sin
c
{\displaystyle AD=\sin c}
A
E
=
sin
b
{\displaystyle AE=\sin b}
ஆனால்
A
A
′
=
A
D
sin
B
=
A
E
sin
C
{\displaystyle AA'=AD\sin B=AE\sin C}
sin
c
sin
B
=
sin
b
sin
C
{\displaystyle \sin c\sin B=\sin b\sin C}
sin
B
sin
b
=
sin
C
sin
c
{\displaystyle {\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}}
இதேபோன்று மற்ற உச்சிகளுக்கும் பெறப்படும் முடிவுகளைக் கொண்டு முழுமையான சைன் விதியைப் பெறலாம்:
sin
A
sin
a
=
sin
B
sin
b
=
sin
C
sin
c
{\displaystyle {\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}}
↑ Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited . Washington, DC: Math. Assoc. Amer., pp. 1–3, 1967
↑ 2.0 2.1 "Law of Sines" . www.pballew.net . Archived from the original on 2018-09-10. Retrieved 2018-09-18 .↑ Mr. T's Math Videos (2015-06-10), Area of a Triangle and Radius of its Circumscribed Circle archived from the original on 2021-12-11, retrieved 2018-09-18 ↑ Mitchell, Douglas W., "A Heron-type area formula in terms of sines," Mathematical Gazette 93, March 2009, 108–109.
↑ Todhunter, I. (1886). Spherical Trigonometry Archived from the original on 2020-04-14. Retrieved 2013-07-28 .





























![{\displaystyle {\begin{aligned}{\frac {abc}{2T}}&={\frac {abc}{2{\sqrt {s(s-a)(s-b)(s-c)}}}}\\[6pt]&={\frac {2abc}{\sqrt {{(a^{2}+b^{2}+c^{2})}^{2}-2(a^{4}+b^{4}+c^{4})}}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0791f9e5aaf7e592ffdd98ae27e4b34555d1a68)







![{\displaystyle {\begin{aligned}\sin ^{2}A&=1-\left({\frac {\cos a-\cos b\cos c}{\sin b\sin c}}\right)^{2}\\[5pt]&={\frac {(1-\cos ^{2}b)(1-\cos ^{2}c)-(\cos a-\cos b\cos c)^{2}}{\sin ^{2}\!b\,\sin ^{2}\!c}}\\[5pt]{\frac {\sin A}{\sin a}}&={\frac {[1-\cos ^{2}\!a-\cos ^{2}\!b-\cos ^{2}\!c+2\cos a\cos b\cos c]^{1/2}}{\sin a\sin b\sin c}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afdaf68867235fdccb09c76fbcb4f2b19d644ddc)

![{\displaystyle {\frac {\sin B}{\sin b}}={\frac {[1-\cos ^{2}\!a-\cos ^{2}\!b-\cos ^{2}\!c+2\cos a\cos b\cos c]^{1/2}}{\sin a\sin b\sin c}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83b0eb9ef515ca1822d69cd58a703543e581720e)
![{\displaystyle {\frac {\sin C}{\sin c}}={\frac {[1-\cos ^{2}\!a-\cos ^{2}\!b-\cos ^{2}\!c+2\cos a\cos b\cos c]^{1/2}}{\sin a\sin b\sin c}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cee9a4213d88e3535cf473b6c49ddf0f31725984)

![{\displaystyle {\begin{aligned}{\bigl (}\mathbf {OA} \cdot (\mathbf {OB} \times \mathbf {OC} ){\bigr )}^{2}&=\left(\det {\begin{pmatrix}\mathbf {OA} &\mathbf {OB} &\mathbf {OC} \end{pmatrix}}\right)^{2}\\[4pt]&={\begin{vmatrix}0&0&1\\\sin c&0&\cos c\\\sin b\cos A&\sin b\sin A&\cos b\end{vmatrix}}^{2}=\left(\sin b\sin c\sin A\right)^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79cea5e52de68d1a8f7e1580b11fc867bdd7daf4)

















