கட்டற்ற கலைக்களஞ்சியமான விக்கிப்பீடியாவில் இருந்து.
மீப்பெரு முழுஎண் சார்பின் வரைபடம் கணிதத்தில் மீப்பெரு முழுஎண் சார்பு (greatest integer function ) என்பது மெய்யெண்களின் மீது வரையறுக்கப்பட்டதொரு சார்பு . இச்சார்பின் கீழ் ஒரு மெய்யெண்ணின் சார்பலன் அம்மெய்யெண்ணை விட சிறிய முழுஎண்களுக்குள் மிகப்பெரிய முழுஎண்ணாகும் [ 1] கீழ்மட்டச் சார்பு (floor function ) எனவும் இச்சார்பு அழைக்கப்படுகிறது. இதன் குறியீடு
⌊
x
⌋
.
{\displaystyle \lfloor x\rfloor .}
எடுத்துக்காட்டுகள்:
⌊
12
5
⌋
{\displaystyle \lfloor {\frac {12}{5}}\rfloor }
⌊
2.4
⌋
=
2
{\displaystyle \lfloor 2.4\rfloor =2}
⌊
2
⌋
=
2
{\displaystyle \lfloor 2\rfloor =2}
⌊
−
2
⌋
=
−
2
{\displaystyle \lfloor -2\rfloor =-2}
⌊
−
2.7
⌋
=
−
3
{\displaystyle \lfloor -2.7\rfloor =-3}
கார்ல் ஃப்ரெடெரிக் காஸ் இருபடி நேர்எதிர்மை -குறித்த தனது மூன்றாவது நிறுவலில் (1808) மீப்பெரு முழுஎண் சார்புக்கு சதுர அடைப்புக் குறியீட்டைப் (
[
x
]
{\displaystyle [x]}
[ 2] மீச்சிறு முழுஎண் சார்பு ஆகிய இரு சார்புகளையும், மற்றும் அவற்றின் குறியீடுகளாக முறையே
⌊
x
⌋
,
{\displaystyle \lfloor x\rfloor ,}
⌈
x
⌉
{\displaystyle \lceil x\rceil }
[ 3] [ 4] [ 5] [ 6]
[ தொகு ] மீப்பெரு முழுஎண் சார்பு பின்வருமாறு வரையறுக்கப்படுகிறது:
⌊
x
⌋
=
max
{
m
∈
Z
∣
m
≤
x
}
{\displaystyle \lfloor x\rfloor =\max \,\{m\in \mathbb {Z} \mid m\leq x\}\,}
ஓரலகு நீளமுள்ள பாதி திறந்த இடைவெளியில் ஒரேயொரு முழுஎண் மட்டுமே இருக்கும் என்பதால், x என்ற மெய்யெண்ணுக்கு,
x
−
1
<
m
≤
x
≤
n
<
x
+
1.
{\displaystyle x-1<m\leq x\leq n<x+1.\;}
என்றவாறு m , n என இரு தனித்த முழுஎண்கள் அமைகின்றன. இதனைப் பயன்படுத்தி மீப்பெரு முழுஎண் சார்பின் வரையறையைப் பின்வருமாறும் கூறலாம்:
⌊
x
⌋
=
m
{\displaystyle \lfloor x\rfloor =m\,}
⌊
x
+
n
⌋
=
⌊
x
⌋
+
n
{\displaystyle \lfloor x+n\rfloor =\lfloor x\rfloor +n\,}
n ஒரு முழு எண்)
⌊
x
⌋
+
⌊
y
⌋
≤
⌊
x
+
y
⌋
≤
⌊
x
⌋
+
⌊
y
⌋
+
1
{\displaystyle \lfloor x\rfloor +\lfloor y\rfloor \leq \lfloor x+y\rfloor \leq \lfloor x\rfloor +\lfloor y\rfloor +1\,}
x , y இரு மெய்யெண்கள்)
⌊
⌊
x
⌋
⌋
=
⌊
x
⌋
{\displaystyle {\Big \lfloor }\lfloor x\rfloor {\Big \rfloor }=\lfloor x\rfloor \,}
தன்னடுக்குச் சார்பு [ தொகு ]
⌊
x
⌋
≤
⌈
x
⌉
{\displaystyle \lfloor x\rfloor \leq \lceil x\rceil \,}
x முழு எண்ணாக இருந்தால், இருந்தால் மட்டுமே, இதில் சமக்குறி உண்மையாகும். அதாவது:
⌈
x
⌉
−
⌊
x
⌋
=
{
0
if
x
∈
Z
1
if
x
∉
Z
{\displaystyle \lceil x\rceil -\lfloor x\rfloor ={\begin{cases}0&{\mbox{ if }}x\in \mathbb {Z} \\1&{\mbox{ if }}x\not \in \mathbb {Z} \end{cases}}\,}
⌊
x
⌋
+
⌈
−
x
⌉
=
0
−
⌊
x
⌋
=
⌈
−
x
⌉
−
⌈
x
⌉
=
⌊
−
x
⌋
{\displaystyle {\begin{aligned}\lfloor x\rfloor +\lceil -x\rceil &=0\\-\lfloor x\rfloor &=\lceil -x\rceil \\-\lceil x\rceil &=\lfloor -x\rfloor \end{aligned}}\,}
⌊
x
⌋
+
⌊
−
x
⌋
=
{
0
if
x
∈
Z
−
1
if
x
∉
Z
,
{\displaystyle \lfloor x\rfloor +\lfloor -x\rfloor ={\begin{cases}0&{\mbox{ if }}x\in \mathbb {Z} \\-1&{\mbox{ if }}x\not \in \mathbb {Z} ,\end{cases}}\,}
⌈
x
⌉
+
⌈
−
x
⌉
=
{
0
if
x
∈
Z
1
if
x
∉
Z
.
{\displaystyle \lceil x\rceil +\lceil -x\rceil ={\begin{cases}0&{\mbox{ if }}x\in \mathbb {Z} \\1&{\mbox{ if }}x\not \in \mathbb {Z} .\end{cases}}\,}
மீப்பெரு முழுஎண் சார்பு தொடர்ச்சியான சார்பல்ல ; எனினும் அது மேல் அரைத்தொடர்ச்சியானதாகவும் துண்டுவாரி மாறிலிச் சார்பாகவும் அமையும். கட்டுரையின் தொடக்கத்தில் தரப்பட்டுள்ள வரைபடத்திலிருந்து இவ் விவரத்தைக் காணலாம்.
↑ Graham, Knuth, & Patashnik, Ch. 3.1
↑ Lemmermeyer, pp. 10, 23.
↑ e.g. Cassels, Hardy & Wright, and Ribenboim use Gauss's notation, Graham, Knuth & Patashnik, and Crandall & Pomerance use Iverson's.
↑ Iverson, p. 12.
↑ Higham, p. 25.
↑ See the Wolfram MathWorld article.
Hazewinkel, Michiel, ed. (2001), "Floor function" , Encyclopedia of Mathematics , Springer, பன்னாட்டுத் தரப்புத்தக எண் 978-1556080104 Štefan Porubský, "Integer rounding functions" , Interactive Information Portal for Algorithmic Mathematics , Institute of Computer Science of the Czech Academy of Sciences, Prague, Czech Republic, retrieved 24 October 2008
Weisstein, Eric W., "Floor Function" , MathWorld . Weisstein, Eric W., "Ceiling Function" , MathWorld . 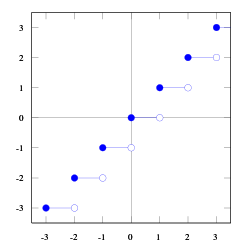







![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)













