இணைகரம்
Appearance

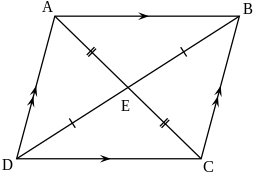
இணைகரம் என்பது நான்கு பக்கங்களைக் கொண்ட ஒரு தள வடிவமாகும். இதன் இரண்டு சோடி எதிர்ப் பக்கங்களும் ஒன்றுக்கொன்று இணையாகவும் (சமாந்தரமாகவும்), சம நீளம் கொண்டவையாகவும் இருக்கும். அத்துடன் இணைகரத்தின் எதிர்க் கோணங்கள் ஒன்றுக்கொன்று சமமாக இருக்கும். ஒவ்வொரு இணைகரமும் ஒரு பல்கோணமாகும். மேலும் குறிப்பாக ஒரு நாற்கரம் ஆகும்.
வேறு வடிவில் சொல்வதானால் சம நீளமான, இரட்டை சமாந்தரக் கோடுகளால் அடைக்கப் பெற்ற வடிவம் இணைகரம் ஆகும், கோணங்கள் செங்கோணம் என்று வரும்போது அவ்விணைகரம் செவ்வகம் என்றும், கோணங்கள் செங்கோணங்களாகவும் அத்துடன், அயற்பக்கங்களும் சமனாக வரும்போது அவ்விணைகரம் சதுரம் என்றும் அழைக்கப்படும்.[1][2][3]
இயல்புகள்
[தொகு]- எதிரெதிர் பக்கங்கள் சமமானவை.
- எதிரெதிர் கோணங்கள் சமமானவை.
- எதிர்ப்பக்கங்கள் ஒருபோதும் இணைவதில்லை.
- இணைகரத்தின் மூலைவிட்டங்கள் ஒன்றையொன்று சமமாக வெட்டும்.
- இணைகரத்தின் பரப்பளவானது அடிப்பக்கத்தை செங்குத்துயரத்தால் பெருக்கி வரும் பெறுமானமாகும்.
- இணைகரத்தின் பரப்பளவானது மூலைவிட்டங்களால் ஏற்படும் இரு முக்கோணங்களின் பரப்பளவின் கூட்டுத் தொகையாகும்.
வகைகள்
[தொகு]- செவ்வகம் - கோணங்களை செங்கோணமாகக் கொண்ட இணைகரம்
- சாய்சதுரம் - நான்கு பக்கங்களும் சமமாகக் கொண்ட இணைகரம்.

- சதுரம் - கோணங்கள் செங்கோணங்களாகவும், நான்கு பக்கங்களும் சமமாகவும் கொண்ட இணைகரம்.
இணைகரத்தின் பரப்பளவு
[தொகு]இணைகரத்தின் பரப்பளவானது அடிப்பக்கத்தை செங்குத்துயரத்தால் பெருக்கி வரும் பெறுமானமாகும்.
A = B X H

மேற்கோள்கள்
[தொகு]- ↑ "CIMT - Page no longer available at Plymouth University servers" (PDF). www.cimt.plymouth.ac.uk. Archived from the original (PDF) on 2014-05-14.
- ↑ Owen Byer, Felix Lazebnik and Deirdre Smeltzer, Methods for Euclidean Geometry, Mathematical Association of America, 2010, pp. 51-52.
- ↑ Zalman Usiskin and Jennifer Griffin, "The Classification of Quadrilaterals. A Study of Definition", Information Age Publishing, 2008, p. 22.